Introduction to Econometrics - Basic principles of probabilities -Definitions of Probability

I.I.1 Definitions of probability

First we want to define the concept of probability. This is quite difficult since there is a lot of disagreement on this matter. Several definitions of probability may be found in literature (ZELLNER in GRILICHES, ZVI and INTRILIGATOR, MICHAEL D. (eds.)):

	Axiomatic definition (De Moivre, J. Neyman): If there are n equally likely possible alternatives, and an event E can happen in m ways out of n, then the probability of occurrence of E (c.q. success) is P(E) = m/n. This definition is circular since it defines probability in terms of itself (c.q. "equally likely" could be interpreted as "equally probable").
	Venn Limit definition (R. Mises): If an event occurs a large number of times, then the probability of p is the limit of the ratio of the number of times when p will be true to the whole number of trials, when the number of trials tends to infinity. The problem in this definition is the fact that an actual limiting number may not exist.
	Hypothetical Infinite Population definition (R. A. Fisher): An actually infinite number of possible trials are assumed. Then the probability of p is defined as the ratio of the number of cases where p is true to the whole number.
	Jeffreys' definition: Probability is the degree of confidence that we may reasonably have in a proposition. This definition is quite vague, but is used in Jeffrey's axiom system. This enables us to derive an axiomatic probability theory.
	Value of Expectation definition: If for an individual the utility of the uncertain outcome of getting a sum of s dollars or zero dollars is the same as getting a sure payment of one dollar, the probability of the uncertain outcome of getting s dollars is defined to be u(1)/u(s), where u(.) is a utility function. If u(.) can be taken proportional to returns, the probability of receiving s is 1/s.

One may think of a set of different possible events as a probability space. This space then represents all possible events, and thus there will always be at least one event in this space that is valid. This thought can also be expressed by saying that the chance of the space itself equals one.

On the other hand the chance of one specific event occurring will always lie between 0 and 1. We denote this as

(where P is used as a symbol for Probability, and Event1 is a specific event in our space). Also the probability of non-occurrence (c.q. failure) is denoted by

.

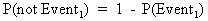Thus, the sum of success and failure of a specific event equals one:

.

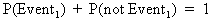The following definitions are commonly used and facilitate nomenclature:

negation

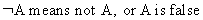
(I.I.1-1)

intersection or conjunction

(I.I.1-2)

union or disjunction

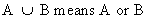
(I.I.1-3)

multiple intersection or conjunction

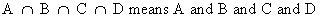
(I.I.1-4)

(all are true)

multiple union or disjunction

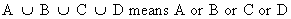
(I.I.1-5)

(at least one is true)

exclusiveness; propositions Ei for i = 1, 2, 3, ..., n are exclusive on data D

if only one of these propositions can be true given data D, or if none of them is true given D

exhaustiveness; propositions Ei for i = 1, 2, 3, ..., n are exhaustive on data D if at least one of these propositions is true given D

if exactly one proposition E_i (for i = 1, 2, 3, ..., n) is true given D, these propositions are said to be exclusive and exhaustive

Furthermore, it is very important to keep in mind that the union of several independent events of the space equals the sum of the individual probabilities of each event. This can symbolically be written as:

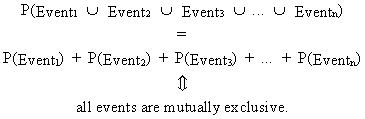
(I.I.1-6)

As in the description of exclusiveness and exhaustiveness, probabilities may exist in a conditional form. Let C and X denote two events then

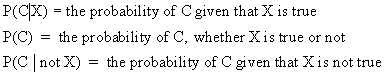
If the validity of X would not have any influence on C this would imply that C would be independent from X. This could be denoted as:

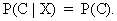
(I.I.1-7)

In case X would have an influence on the occurrence of C (dependence), we would write

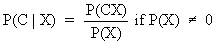
(I.I.1-8)

where P(C X) is the probability of C and X occurring at the same time.

This property is so important that the reader is asked to bear it mind! Also, this property is very useful to prove Bayes' theorem.

In the special case where

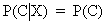
eq. (I.I.1-8) can be rewritten as P(C X) = P(C) P(X) (if C and X are independent events).

The generalized form of eq. (I.I.1-8) is

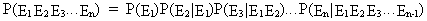
(I.I.1-9)

and in the special case where all events are independent

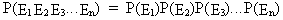
(I.I.1-10)