III.I.1 Heteroskedasticity in
Linear Regression
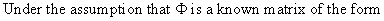
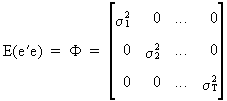
(III.I.1-1)
we can
use a two step procedure to solve the problem of heteroskedasticity
as follows:
 | divide
each observation by the S.D. of the error term for that
observation | |
 | apply
LS to the transformed observations | |
This
procedure is called the Weighted
Least Squares (WLS).
Of
course there exist a lot of alternative transformations. One of the
most popular transformations is the Neperian logarithm, since it
gives more weight to small-valued observations and less weight to
large ones. The transformation of time series according to the
logarithmic and related transformations is (in econometrics) mostly
assumed to be theory-related.
Another
method is specially designed to solve the problem of multiplicative
heteroskedasticity.
Suppose
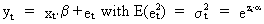
(III.I.1-2)

From
(III.I.1-2) we find
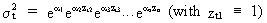
(III.I.1-3)
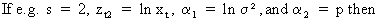
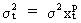
(III.I.1-4)
The
only question remaining is "How to estimate alpha?".
We
may rewrite (III.I.1-2) by taking logarithms
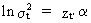
(III.I.1-5)
and
since
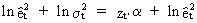
(III.I.1-6)
it
is obvious that
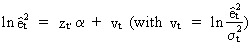
(III.I.1-7)
Now
we put all t elements from (III.I.1-7) in matrices and obtain
estimates of alpha for the model
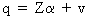
(III.I.1-8)
by
solving
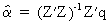
(III.I.1-9)
Once
the alpha parameter vector has been computed this information can be
used in the following Estimated
Generalized Least Squares estimator (EGLS)
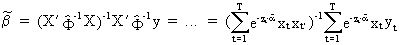
(III.I.1-10)
Consider
the following multiple regression equation (to be used in subsequent
illustrations):
Estimation
with OLS:
Endogenous
variable = ship.dba
Variable
Parameter
S.E. t-stat
const(-0),1.,0,0
+294.5647227 247.2103565
+1.19
employ(-0),1.,0,0
+34.36683831 5.160885579
+6.66
expend(-0),1.,0,0
+9.572870953 2.108664727
+4.54
2-tail-t
at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
R-squared of stationary series = 0.9193525203
Durbin-Watson = 2.472087712
Variance of regression = 1051039.479
Standard Error of regression = 1025.202165
Sum of Squared Residuals = 37837421.25
Degrees of freedom = 36
Correlation
matrix of parameters:
+1.00 -0.42 +0.03
-0.42 +1.00 -0.85
+0.03 -0.85 +1.00
Detection
of heteroskedasticity can be achieved by many different tests.
If we assume a linear statistical model of the form
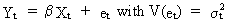
(III.I.1-11)
then
a test for heteroskedasticity, according to Glejser,
can be obtained by testing
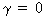
in
one of the following models
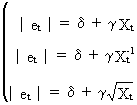
(III.I.1-12)
(and
many others...).
Warning:
this test should only be used if the endogenous variable is NOT used
as lagged exogenous variable. Furthermore the Gleisjer tests assume
ADDITIVE heteroskedasticity. All OLS assumptions should be
satisfied.
Below
you ‘ll find an example of how Gleisjer tests can be applied to
test for heteroskedasticity (this test is applied to our
example-equation):
Gleisjer
tests:
Estimation
with OLS:
Endogenous
variable = abs(e)
Variable
Parameter
S.E. t-stat
const(-0),1.,0,0
+186.2884948 148.8382962
+1.25
employ(-0),1.,0,0
+7.009636535 1.65355995
+4.24
2-tail-t
at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
R-squared
of stationary series = 0.3392877362
Durbin-Watson = 2.107710811
Degrees of freedom
= 37
Variance
of regression = 381232.1935
Standard Error of regression = 617.4400323
Sum of Squared Residuals
= 14105591.16
Correlation
matrix of parameters:
+1.00 -0.75
-0.75 +1.00
T-STAT
of b in abs(e) =
a + b X = 4.239118477
Estimation
with OLS:
Endogenous
variable = abs(e)
Variable
Parameter
S.E. t-stat
const(-0),1.,0,0
+247.1919656 131.7411655
+1.88
expend(-0),1.,0,0
+3.009214899 0.658345735
+4.57
2-tail-t
at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
R-squared
of stationary series = 0.3613379003
Durbin-Watson = 1.709541158
Degrees of freedom
= 37
Variance
of regression = 361985.459
Standard Error of regression = 601.6522741
Sum of Squared Residuals
= 13393461.98
Correlation
matrix of parameters:
+1.00 -0.68
-0.68 +1.00
T-STAT
of b in abs(e) =
a + b X = 4.570873234
Estimation
with OLS:
Endogenous
variable = abs(e)
Variable
Parameter
S.E. t-stat
const(-0),1.,0,0
+1453.542646 204.7255451
+7.1
employ(-0),1.,0,0
-34269.28262 7753.841264
-4.42
2-tail-t
at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
R-squared
of stationary series = 0.3458859921
Durbin-Watson = 1.762971931
Degrees of freedom
= 37
Variance
of regression = 370690.754
Standard Error of regression = 608.8437845
Sum of Squared Residuals
= 13715557.9
Correlation
matrix of parameters:
+1.00 -0.88
-0.88 +1.00
T-STAT
of b in abs(e) =
a + b 1/X = -4.419652331
Estimation
with OLS:
Endogenous
variable = abs(e)
Variable
Parameter
S.E. t-stat
const(-0),1.,0,0
+1296.342082 182.4520168
+7.11
expend(-0),1.,0,0
-42579.02335 10204.88361
-4.17
2-tail-t
at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
R-squared
of stationary series = 0.3203453806
Durbin-Watson = 1.553508102
Degrees of freedom
= 37
Variance
of regression = 385163.4666
Standard Error of regression = 620.6153935
Sum of Squared Residuals
= 14251048.26
Correlation
matrix of parameters:
+1.00 -0.84
-0.84 +1.00
T-STAT
of b in abs(e) =
a + b 1/X = -4.172416362
Estimation
with OLS:
Endogenous
variable = abs(e)
Variable
Parameter
S.E. t-stat
const(-0),1.,0,0
-566.1796621 258.3961199
-2.19
employ(-0),1.,0,0
+159.8350094 31.50187299
+5.07
2-tail-t
at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
R-squared
of stationary series = 0.4106281997
Durbin-Watson = 2.169617364
Degrees of freedom
= 37
Variance
of regression = 333999.7394
Standard Error of regression = 577.9271056
Sum of Squared Residuals
= 12357990.36
Correlation
matrix of parameters:
+1.00 -0.93
-0.93 +1.00
T-STAT
of b in abs(e) =
a + b sqrt(X) = 5.073825594
Estimation
with OLS:
Endogenous
variable = abs(e)
Variable
Parameter
S.E. t-stat
const(-0),1.,0,0
-318.6307381 205.1846763
-1.55
expend(-0),1.,0,0
+93.21309421 17.56301183
+5.31
2-tail-t
at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
R-squared
of stationary series = 0.4325531446
Durbin-Watson = 1.866343044
Degrees of freedom
= 37
Variance
of regression = 321574.7705
Standard Error of regression = 567.0756303
Sum of Squared Residuals
= 11898266.51
Correlation
matrix of parameters:
+1.00 -0.90
-0.90 +1.00
T-STAT
of b in abs(e) =
a + b sqrt(X) = 5.30735247
Estimation
with OLS:
Endogenous
variable = abs(e)
Variable
Parameter
S.E. t-stat
const(-0),1.,0,0
+186.2884948 148.8382962
+1.25
employ(-0),1.,0,0
+7.009636535 1.65355995
+4.24
2-tail-t
at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
R-squared
of stationary series = 0.3272823951
Durbin-Watson = 2.107710811
Degrees of freedom
= 37
Variance
of regression = 381232.1935
Standard Error of regression = 617.4400323
Sum of Squared Residuals
= 14105591.16
Correlation
matrix of parameters:
+1.00 -0.75
-0.75 +1.00
T-STAT
of b in abs(e) =
a + b abs(X) = 4.239118477
Estimation
with OLS:
Endogenous
variable = abs(e)
Variable
Parameter
S.E. t-stat
const(-0),1.,0,0
+247.1919656 131.7411655
+1.88
expend(-0),1.,0,0
+3.009214899 0.658345735
+4.57
2-tail-t
at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
R-squared
of stationary series = 0.3612449444
Durbin-Watson = 1.709541158
Degrees of freedom
= 37
Variance
of regression = 361985.459
Standard Error of regression = 601.6522741
Sum of Squared Residuals
= 13393461.98
Correlation
matrix of parameters:
+1.00 -0.68
-0.68 +1.00
T-STAT
of b in abs(e) =
a + b abs(X) = 4.570873234
Estimation
with OLS:
Endogenous
variable = abs(e)
Variable
Parameter
S.E.
t-stat
const(-0),1.,0,0
+534.6889586
121.5421391
+4.4
employ(-0),1.,0,0
+1.52089658e-002 6.025380217e-003
+2.52
2-tail-t
at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
R-squared
of stationary series = 0.1473776172
Durbin-Watson = 1.732573146
Degrees of freedom
= 37
Variance
of regression = 483185.0673
Standard Error of regression = 695.1151468
Sum of Squared Residuals
= 17877847.49
Correlation
matrix of parameters:
+1.00 -0.40
-0.40 +1.00
T-STAT
of b in abs(e) =
a + b X*X = 2.524150387
Estimation
with OLS:
Endogenous
variable = abs(e)
Variable
Parameter
S.E. t-stat
const(-0),1.,0,0
+509.6383822
120.1542444 +4.24
expend(-0),1.,0,0
+3.702769252e-003 1.275457967e-003
+2.9
2-tail-t
at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
R-squared
of stationary series = 0.1859772184
Durbin-Watson = 1.408225521
Degrees of freedom
= 37
Variance
of regression = 461310.494
Standard Error of regression = 679.1984202
Sum of Squared Residuals
= 17068488.28
Correlation
matrix of parameters:
+1.00 -0.43
-0.43 +1.00
T-STAT
of b in abs(e) =
a + b X*X = 2.903089987
Another
popular test is the so-called likelihood ratio test for heteroskedasticity
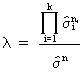
(III.I.1-13)

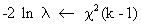
(III.I.1-14)
which
can be used for testing statistical significance.
The
Goldfeld-Quandt test for
heteroskedasticity uses test-equations for each exogenous variable
(except the constant term). This test is widely applicable, and
fairly unproblematic w.r.t. it’s properties. The Goldfeld-Quandt
test uses two regressions of the endogenous variable on each
variable separately; the first regression is based on LOW values of
the exogenous variable, the second regression is based on HIGH
values of the exogenous variable. Note that a pre-specified number
of values in-between LOW and HIGH values are NOT used in these
regressions.
Below
you ‘ll find an example of how the Goldfeld-Quandt test can be
applied to test for heteroskedasticity (this test is applied to our
example-equation):
Goldfeld-Quandt
Test
The
Goldfeld-Quandt test will be based on two regressions of (T - 13)/2 observations.
The first regression on low values of Xi, the second on high values
of Xi.
Estimation
with OLS:
Endogenous
variable = ship.dba
Variable
Parameter
S.E. t-stat
const(-0),1.,0,0
+1795.714286 130.620347
+13.7
2-tail-t
at 95 percent = 2.16
1-tail-t at 95 percent = 1.771
R-squared
of stationary series = 0.2605089242
Durbin-Watson = 2.718602812
Degrees of freedom
= 13
Variance
of regression = 238863.4505
Standard Error of regression = 488.7365861
Sum of Squared Residuals
= 3105224.857
Estimation
with OLS:
Endogenous
variable = ship.dba
Variable
Parameter
S.E.
t-stat
const(-0),1.,0,0
+6985.071429 1153.776244
+6.05
2-tail-t
at 95 percent = 2.16
1-tail-t at 95 percent = 1.771
R-squared
of stationary series = 1.268073674e-003
Durbin-Watson = 1.01313106
Degrees of freedom
= 13
Variance
of regression = 18636794.69
Standard Error of regression = 4317.035405
Sum of Squared Residuals
= 242278330.9
Goldfeld-Quandt
test for exogenous variable nr. 1 = 78.02279773
DF of numerator = DF of denominator.
Approximate F critical value (95%) (df = {13,13}) = 2.4
Estimation
with OLS:
Endogenous
variable = ship.dba
Variable
Parameter
S.E. t-stat
employ(-0),1.,0,0
+62.53440159 2.987781852
+20.9
2-tail-t
at 95 percent = 2.16
1-tail-t at 95 percent = 1.771
R-squared
of stationary series = 0.9195408482
Durbin-Watson = 1.804461765
Degrees of freedom
= 13
Variance
of regression = 98605.87903
Standard Error of regression = 314.0157305
Sum of Squared Residuals
= 1281876.427
Estimation
with OLS:
Endogenous
variable = ship.dba
Variable
Parameter
S.E. t-stat
employ(-0),1.,0,0
+56.49942486 3.939457673
+14.3
2-tail-t
at 95 percent = 2.16
1-tail-t at 95 percent = 1.771
R-squared
of stationary series = 1.003004769
Durbin-Watson = 1.178141189
Degrees of freedom
= 13
Variance
of regression = 4357873.512
Standard Error of regression = 2087.552038
Sum of Squared Residuals
= 56652355.66
Goldfeld-Quandt
test for exogenous variable nr. 2 = 44.194865
DF of numerator = DF of denominator.
Approximate F critical value (95%) (df = {13,13}) = 2.4
Estimation
with OLS:
Endogenous
variable = ship.dba
Variable
Parameter
S.E. t-stat
expend(-0),1.,0,0
+43.94765568
3.306817926
+13.3
2-tail-t
at 95 percent = 2.16
1-tail-t at 95 percent = 1.771
R-squared
of stationary series = 0.8503625979
Durbin-Watson = 2.958320856
Degrees of freedom
= 13
Variance
of regression = 254447.5573
Standard Error of regression = 504.4279505
Sum of Squared Residuals
= 3307818.245
Estimation
with OLS:
Endogenous
variable = ship.dba
Variable
Parameter
S.E.
t-stat
expend(-0),1.,0,0
+24.00368738
1.992895783
+12.
2-tail-t
at 95 percent = 2.16
1-tail-t at 95 percent = 1.771
R-squared
of stationary series = 0.8703061351
Durbin-Watson = 2.720031672
Degrees of freedom
= 13
Variance
of regression = 5853973.458
Standard Error of regression = 2419.498596
Sum of Squared Residuals
= 76101654.96
Goldfeld-Quandt
test for exogenous variable nr. 3 = 23.00660113
DF of numerator = DF of denominator.
Approximate F critical value (95%) (df = {13,13}) = 2.4
The
Park tests for
heteroskedasticity uses a test-equation for each exogenous variable:
the logarithms of squared residuals are explained by the logarithm
of the absolute values of the exogenous variable.
Warning:
this test should only be used if the endogenous variable is NOT used
as lagged exogenous variable. Furthermore the Park tests assume
MULTIPLICATIVE heteroskedasticity. All OLS assumptions should be
satisfied.
Below
you will find an example of how the Park test can be applied to test
for heteroskedasticity (this test is applied to our example-equation):
T-STAT
values of b in Simple Regression:
Estimation
with OLS:
Endogenous
variable = ln(e*e)
Variable
Parameter
S.E. t-stat
const(-0),1.,0,0
+2.673616498 2.32005065
+1.15
employ(-0),1.,0,0
+2.255741073 0.5790504391
+3.9
2-tail-t
at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
T-STAT of b in
ln(e*e) = a + b ln abs(X) = 3.8955865
Estimation
with OLS:
Endogenous
variable = ln(e*e)
Variable
Parameter
S.E. t-stat
const(-0),1.,0,0
+3.990749162
2.084773124
+1.91
expend(-0),1.,0,0
+1.688936824 0.4553619992
+3.71
2-tail-t
at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
T-STAT of b in
ln(e*e) = a + b ln abs(X) = 3.708998175
The
Breusch-Pagan test for
heteroskedasticity uses a test-equation: the squared residuals
divided by the residual variance are explained by all exogenous
variables. The test statistic is computed as half the difference
between the Total Sum of Squares and the Sum of Squared Residuals,
which has a Chi-square distribution.
Warning:
this test should only be used if the endogenous variable is NOT used
as lagged exogenous variable AND if the number of observations is
VERY LARGE. All OLS assumptions should be satisfied, including
normality of the error term.
Below
you ‘ll find an example of how the Breusch-Pagan test can be
applied to test for heteroskedasticity (this test is applied to our
example-equation):
Breusch-Pagan
test:
Estimation
with OLS:
Endogenous
variable = ê²/(var(ê))
Variable
Parameter
S.E. t-stat
const(-0),1.,0,0
-5.59940532e-002 0.3553661
-0.158 employ(-0),1.,0,0
+9.716468615e-004 7.418798335e-003 +0.131
expend(-0),1.,0,0
+6.694376613e-003 3.031215889e-003
+2.21
2-tail-t
at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
R-squared
of stationary series = 0.9998009501
Durbin-Watson = 2.041789465
Degrees of freedom
= 36
Variance
of regression = 2.171889371
Standard Error of regression = 1.473733141
Sum of Squared Residuals
= 78.18801734
regression:
e_hat**2/(var(e_hat)) = a + X b + v
residual
variance = 2.171889371
(TSS-SSR)/2 = 39.35189667
Chi-square (95 percent) critical value = 5.99
The
Squared Residuals versus
Squared Fit test for heteroskedasticity uses a test-equation:
the squared residuals are explained by the squared interpolation
forecast of the original regression. This test is fairly
unproblematic and can be used in almost all cases. The t-statistic
of the Squared-Fit-parameter indicates whether heteroskedasticity is
present or not.
Below
you ‘ll find an example of how the Squared Residuals versus
Squared Fit test can be
applied to test for heteroskedasticity (this test is applied to our
example-equation):
Squared Residuals versus
Squared Fit:
Estimation with OLS:
Endogenous variable =
SquaredResiduals
Variable
Parameter
S.E.
t-stat
constant(-0),1.,0,0
+592305.4721
312179.7592
+1.9
SquaredFit(-1),1.,0,0 +1.432760191e-002
5.425552377e-003 +2.64
2-tail-t at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
R-squared of stationary series
= 0.1585866958 Durbin-Watson
= 2.020505492
Degrees of freedom = 37
Variance
of regression = 3.002200902e+012
Standard Error of regression = 1732686.037
Sum of Squared Residuals = 1.110814334e+014
Correlation matrix of
parameters:
+1.00 -0.46
-0.46 +1.00
regression:
e_hat*e_hat = a + y_hat*y_hat*b + v
The
ARCH(p) test is used to
test for Autoregressive Conditional Heteroskedasticity: the squared
residuals are explained by it’s lagged values (p is the number of
lags included in the test-equation). The presence of Conditional
Heteroskedasticity is tested by the use of an F-statistic.
Below
you ‘ll find an example of how the ARCH(p)
test can be applied to test for Conditional Heteroskedasticity
(this test is applied to our example-equation):
Arch(p) test by Least Squares:
Estimation with OLS:
Endogenous variable =
SquaredResiduals
Variable
Parameter
S.E.
t-stat
constant(-0),1.,0,0
+362168.8873
318289.0843
+1.14
SqResid(-1),1.,0,0
+5.744398869e-002 0.1786811315
+0.321
SqResid(-2),1.,0,0
+0.4790710887
0.1723985422
+2.78
SqResid(-3),1.,0,0
+0.2166609567
0.1908881265
+1.14
2-tail-t at 95 percent = 2.042
1-tail-t at 95 percent = 1.697
R-squared of stationary series
= 0.3602748235 Durbin-Watson
= 1.823445676
Degrees of freedom = 32
Variance
of regression = 2.594323444e+012
Standard Error of regression = 1610690.363
Sum of Squared Residuals = 8.301835022e+013
Correlation matrix of
parameters:
+1.00 -0.21 -0.22 -0.11
-0.21 +1.00 -0.25 -0.48
-0.22 -0.25 +1.00 -0.24
-0.11 -0.48 -0.24 +1.00
F-stat = 6.007159936
Critical F value (95%) = 2.84
| 
