Time Series Analysis - ARIMA models - Some remarks and model extensions

V.I.5 Some remarks and model extensions of the ARIMA model

a. Seasonality

The previously described techniques (for ARIMA model building) can be easily expanded for seasonal time series. In fact all identification, estimation, checking, and forecasting procedures are not different from the non-seasonal counterpart. All the above descriptions and reflections are still valid for the seasonal case: one only has to substitute the time lag i (in t-i) for i*s (to obtain an index t-i*s) where s is the seasonal period (e.g. s = 12 for monthly, and s = 4 for quarterly data).

There are two possible ways to combine the non-seasonal and seasonal ARIMA structures into one model.

First an additive seasonality model could be considered

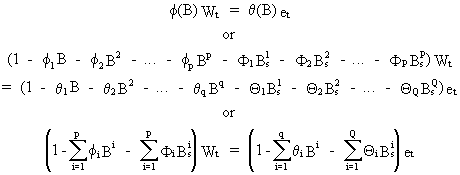
(V.I.5-1)

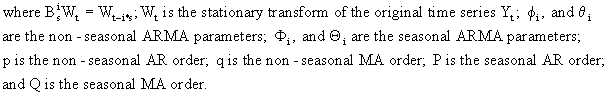
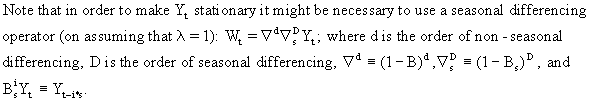
Second, a multiplicative seasonality model could be considered

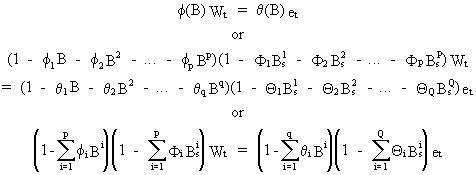
(V.I.5-2)

which is a model containing several (implicit) restrictions on the parameters. This is the standard model which is used, because it takes into account the interaction between seasonal and non-seasonal ARIMA structures: this can be seen by the simple fact that seasonal and non-seasonal parameters are multiplied (on writing the explicit forecast function).

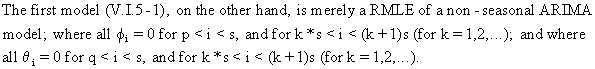
b. Nonlinearity

ARIMA models are capable of modeling some nonlinearities, since they involve (if a seasonal or non-seasonal MA part is present) rational lag structures in terms of the error

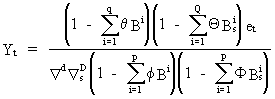
(V.I.5-3)

Due to Wold's decomp. theorem this should suffice to model a stationary time series adequately. It is however possible that another (nonlinear) specification yields a better model, w.r.t. parameter parsimony for certain time series (e.g. a combination of some distributed lag models).

The main reason however, why these alternatives are not successful, is the simple fact that ARIMA models can be built according to the Box-Jenkins methodology which is a comprehensive, general, and widely applicable procedure, involving many possible diagnostic identification tools; theoretical (mathematical) structures that are easily proved; many checking procedures; and means for model criticism, monitoring, and control. Above that, the Box-Jenkins methodology also suggests means of expanding ARIMA models with the information of exogenous variables (c.q. transfer function).

c. Variable parameters and the Kalman Filter

It is possible to model and estimate ARIMA models where the ARMA parameters (and sometimes even the l parameter) are simultaneously estimated, allowing for (smooth) parameter changes over time. This can be done on using a recursive approach (c.q. estimating parameters for a short sample, and iteratively expanding by one observation such that the parameters can be re-estimated), or on using the famous recursion formulae due to Kalman (see also HARVEY 1989, and his program STAMP).