|
As defined earlier
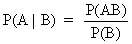
(I.II.1)
and of course
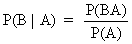
(I.II.2)
Since P(A B) = P(B A) it follows by
substituting (I.II.2) into (I.II.1) that
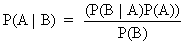
(I.II.3)
Equation (I.II.3) shows clearly that the
chance of A given B can be expressed as a function of the chance of
B given A!
The left hand side of (I.II.3) is called the
posterior probability,
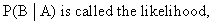
P(A) is called the prior probability, and
P(B) is the probability of B whether A is true or not.
It is quite obvious that (I.II.3) can be
rewritten as:
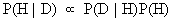
(I.II.4)
where A has been replaced by H (a
hypothesis) and B by D (observed data).
In other words: the probability of the
hypothesis being true, given the fact that specific data have been
observed, varies with the likelihood of the observed data when the
hypothesis is true times the prior probability (subjective
probability) of the hypothesis.
As a matter of fact, equation (I.II.4) is a
simplified version of Bayes' theorem. By extending (I.II.4) just a
little bit, a very useful equation can be found. In fact one only
has to think of two different hypotheses Hyp1 and Hyp2 and apply
equation (I.II.4) to them.
It is easily found that
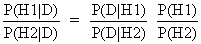
(I.II.5)
or
in words: the posterior odds equal the likelihood ratio multiplied
by the prior odds (Bayes' theorem).
The only question remaining is: how can this
theorem be applied usefully in practice? A very simple example
should clarify the usefulness of this theorem.
Suppose that there are two sacks of gold and
silver coins. Both have been shuffled thoroughly. Denote the first
sack as Hyp1 and the second as Hyp2. Furthermore, it is known that
in the first sack there are 150 gold coins and only 50 silver coins,
in the other sack there are 100 and 200 coins respectively.
Suppose that one had the opportunity to draw
a coin out of one sack, and suppose that one
would pick a gold coin. What is the chance of the drawn coin
to come from the first sack?
Assuming that both sacks have the same chance of being
picked, not regarded the outcome of the drawing, this problem can be
solved quite easily by applying Bayes' theorem as follows:
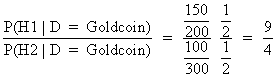
(I.II.6)
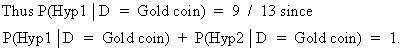
An important issue, when applying Bayes'
theorem or Bayes' regression techniques is that there always is a
subjective (prior) probability that is being incorporated in solving
the problem. This can be of great importance (e.g., if the
researcher has expert knowledge on some events and can therefore influence the outcome of the investigation with his "a
priori" assumptions/knowledge). At the same time this prior probability
could be regarded as an immense drawback when wrongly used or
interpreted.
From now on the discussion of classical
econometrics will be our primary target. The classical approach does
not use a priori knowledge to the full extent as in the Bayes'
method, even if there are important economic theories that are known
to be true.
From now on the economic theory will only be
used as a guideline for econometric specifications and checking of
econometric models a posteriori.
| 
